Funciones

VBA Remoción de Outliers

Posted on by YorsH

Muchas veces los datos que queremos analizar o proyectar incluyen valores que no son representativos del proceso que queremos modelar. Son los denominados outliers, datos excepcionales que no se originan en el proceso estándar: ventas extraordinarias, rendimientos excepcionales, errores no corregidos, puestas en marcha…, etcétera.

¿Qué es un outlier? Un outlier (valor atípico) es todo número que se encuentra a mucha distancia del resto de los datos y que, no siendo un elemento representativo de la población, tiene el potencial de distorsionar el análisis estadístico o la proyección de la serie.

Antes de continuar, es muy importante distinguir entre outliers y los denominados cisnes negros. El concepto cisne negro fue acuñado por Nassim Nicholas Taleb en su libro homónimo del 2007. En él se compara a los eventos raros, impredecibles y con un impacto desproporcionado, con la primera aparición de un cisne negro, antes que la comunidad científica supiera de la existencia de estas aves.

La principal diferencia entre un outlier y un cisne negro es que este último sí hace parte del proceso que se quiere modelar o analizar y por lo tanto ¡no se puede eliminar!. Un cisne negro es un evento muy raro pero que puede eventualmente ocurrir. Y aunque poco probable, su impacto es tan grande que el riesgo de no incluirlo en el análisis se vuelve intolerable.

Muchas veces lo que determina que un evento excepcional sea un outlier o un cisne negro es el objetivo del estudio. Si deseamos pronosticar ventas futuras de clientes actuales, es probable que cualquier evento atípico del pasado e improbable en el futuro no sea algo que necesitemos contabilizar como parte de nuestros flujos de caja esperados. Sin embargo, el mismo evento inesperado sí puede que sea necesario incluirlo cuando estamos planificando compras o producciones en el mediano o largo plazo, puesto que de repetirse podría generar un quiebre de stock eventualmente oneroso.

De esta manera, surgen dos preguntas claves antes de descartar outliers: ¿cuál puede ser el impacto de no considerarlos? Podría darse el caso que el objetivo del modelamiento se vea comprometido al excluir ciertos datos, como sucede con los modelos de quiebres de stock o de liquidez. La segunda pregunta es: ¿qué información estoy dejando de analizar? Un outlier podría contener las pistas que estamos buscando para tener un desempeño excepcional o para evitar errores costosos. Lo más prudente entonces es excluirlos para luego analizarlos por separado y aprender de ellos.

Nos hemos propuesto diseñar una función en VBA que nos permita leer una serie o rango de datos relacionados entre sí por un proceso en común e identificar aquellos valores que se encuentran muy alejados del resto de la población. El objetivo es utilizar esta función como un proceso de limpieza previo al cálculo de estadígrafos y proyecciones que pretendan modelar el comportamiento de la población central. Y una vez identificados los potenciales outliers, pediremos a nuestra función que los reemplace por el valor más cercano (o por la media de los valores más cercanos). De esta manera devolveremos una nueva serie de datos de igual longitud, pero libre de valores atípicos y lista para su uso.

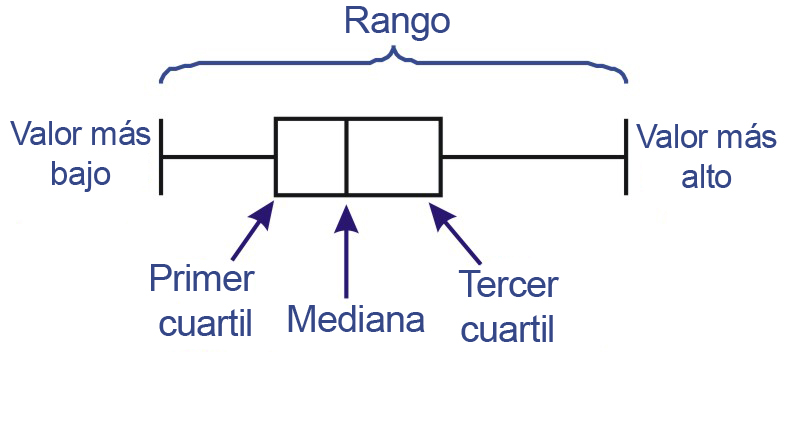
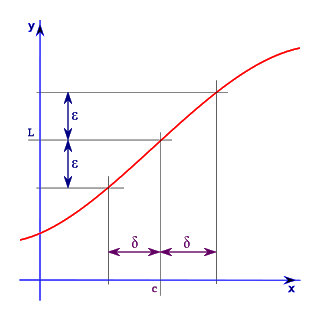
Diagrama de cajas y bigotes para una serie sin outliers

Usaremos el rango intercuartil (IQR) para establecer qué valores son o no atípicos dentro de una muestra de datos. Si ordenamos todos los valores de menor a mayor y los ubicamos a lo largo de una recta, probablemente observaremos cómo los datos tienden a concentrarse en torno a su mediana, distribuyéndose con mayor o menor homogeneidad a ambos costados de ella. Si encerramos en una caja horizontal los valores que se encuentran entre el 25% y el 75% más bajo (percentiles 25 y 75 respectivamente), y consignamos con una raya vertical la posición de la mediana (percentil 50) , obtenemos un diagrama de cajas y bigotes como el mostrado en la figura anterior.

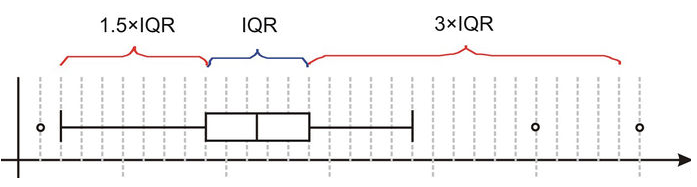
El ancho de la caja (la distancia entre el percentil 25 y el percentil 75), se denomina rango intercuartil (IQR). Si nos desplazamos 1,5 IQR a la izquierda del borde izquierdo de la caja y 1,5 IQR a la derecha del borde derecho de la caja, tendremos dos límites dentro de los cuales debiera encontrarse la gran mayoría de los datos de la población (idealmente todos).

Los valores que se encuentren al exterior de estas marcas serán denominados outliers. Si consideramos como límites 3,0 IQR a la izquierda y a la derecha de la caja, entonces todos aquellos valores al exterior de estos nuevos límites serán denominados outliers extremos.

Comenzamos definiendo una nueva función pública en VBA que denominaremos LIMPIARDATOS. Como parámetros, especificaremos un rango de datos de entrada y una variable lógica (boolean) opcional que marcaremos como verdadero si queremos considerar solamente outliers extremos (por defecto se asume falsa y consideraremos todos los outliers).

Public Function LIMPIARDATOS(ByVal rngDatos As Range, _
    Optional ByVal bolExtremo As Boolean) As Variant

    'Declaramos las variables que utilizarmos en la lectura de datos
    Dim arrDatos() As Double
    Dim i As Integer
    Dim j As Integer
    Dim rngCelda As Range
    
    'Declaramos el arreglo donde almacenaremos la serie de datos limpia
    Dim arrLimpios() As Double
    
    'Declaramos las variables que utilizaremos en la identificación
    Dim dblP25, dblP50, dblP75, dblIQR, dblFactor As Double

    'Declaramos las variables que utilizaremos en la limpieza de outliers
    Dim dblInferior, dblSuperior As Double
    Dim dblIzquierda, dblDerecha As Double
    Dim bolIzquierda, bolDerecha As Boolean
    
    'Leemos los datos en al arreglo arrDatos (horizontal)
    ReDim arrDatos(1 To rngDatos.Count)
    i = 1
    For Each rngCelda In rngDatos
        arrDatos(i) = rngCelda.Value
        i = i + 1
    Next rngCelda
    ReDim arrLimpios(1 To rngDatos.Count)

Para calcular los percentiles (25, 50 y 75) requeridos para estimar el IQR, utilizaremos el método Percentile incorporado en la hoja de cálculo. Luego estimaremos el límite representativo de la población usando un factor de 1,5 o 3,0 veces el IQR según haya sido especificado en la variable bolExtremo pasada por parámetro.

   'Calculamos los distintos cuartiles y el rango intercuartil
   dblP25 = WorksheetFunction.Percentile(arrDatos, 0.25)
   dblP50 = WorksheetFunction.Percentile(arrDatos, 0.5)
   dblP75 = WorksheetFunction.Percentile(arrDatos, 0.75)
   dblIQR = dblP75 - dblP25

   If bolExtremo Then
      'Solo removeremos outliers extremos (3,0 * IQR)
      dblFactor = 3
   Else
      'Removeremos outliers desde 1,5 * IQR (por defecto)
      dblFactor = 1.5
   End If

   'Calculamos limite inferior y superior a partir de los cuales  
   'removeremos los outliers
   dblInferior = dblP25 - dblFactor * dblIQR
   dblSuperior = dblP75 + dblFactor * dblIQR

La segunda parte de nuestra función consiste en recorrer cada uno de los datos del arreglo buscando valores que estén por debajo o por sobre estos límites definidos: arrDatos(i) < dblInferior OR arrDatos(i) > dblSuperior .

Cada vez que encontramos un nuevo outlier deberemos reemplazarlo por el promedio de los valores típicos más cercanos. Si no existen valores típicos a la izquierda, se usará el valor típico más cercano a la derecha. Si no existen valores típicos a la derecha, se usará el valor típico más próximo a la izquierda. Si existen valores típicos a ambos lados, se reemplaza el outlier por el promedio de ambos.

Para hacer esto, cada vez que se encuentra un nuevo outlier, se inicia una búsqueda hacia la izquierda mediante un ciclo Do…Loop. Se itera hasta alcanzar el límite izquierdo del arreglo o hasta que se dé con un valor representativo que podamos usar para reemplazar. Si encontramos un dato con tales características, lo almacenamos en la variable dblIzquierda y marcamos la búsqueda como exitosa (True) usando la variable bolIzquierda. Finalizado este proceso repetimos la búsqueda, pero esta vez hacia la derecha. Reemplazado el outlier encontrado, continuamos con la revisión del siguiente dato de la serie hasta recorrer todo el arreglo.

   'Recorremos el arreglo buscando outliers
   For i = LBound(arrDatos) To UBound(arrDatos)

      'Por defecto copiamos el mismo valor de la serie
      arrLimpios(i) = arrDatos(i)

         If arrDatos(i) < dblInferior Or arrDatos(i) > dblSuperior Then

           'Hemos encontrado un outlier!
           bolIzquierda = False
           bolDerecha = False

           'Buscamos el primer no outlier a la izquierda
           j = i
           Do While j > LBound(arrDatos) And Not bolIzquierda
             j = j - 1
             If arrDatos(j) >= dblInferior And arrDatos(j) <= dblSuperior _ 
              Then
                 'Encontramos un no outlier a la izquierda!
                 bolIzquierda = True
                 dblIzquierda = arrDatos(j)
              End If
           Loop

          'Buscamos el primer no outlier a la derecha
          j = i
          Do While j < UBound(arrDatos) And Not bolDerecha
            j = j + 1
            If arrDatos(j) >= dblInferior And arrDatos(j) <= dblSuperior _
             Then
                'Encontramos un no outlier a la derecha!
                bolDerecha = True
                dblDerecha = arrDatos(j)
            End If
          Loop

       'Calculamos un nuevo valor promediando los valores izquierda y 
       'derecha, si existen
       If bolIzquierda And bolDerecha Then
          arrLimpios(i) = (dblIzquierda + dblDerecha) / 2
       ElseIf bolIzquierda And Not bolDerecha Then
          arrLimpios(i) = dblIzquierda
       ElseIf bolDerecha And Not bolIzquierda Then
          arrLimpios(i) = dblDerecha
       End If

   End If

Next i

De esta forma, hemos trasvasijado el arreglo arrDatos() en el nuevo arreglo arrLimpios(), que contiene sustitutos para los outliers que pudiera contener la serie original. Finalizamos la función devolviendo esta nueva serie como resultado.

    LIMPIARDATOS = arrLimpios
    
End Function

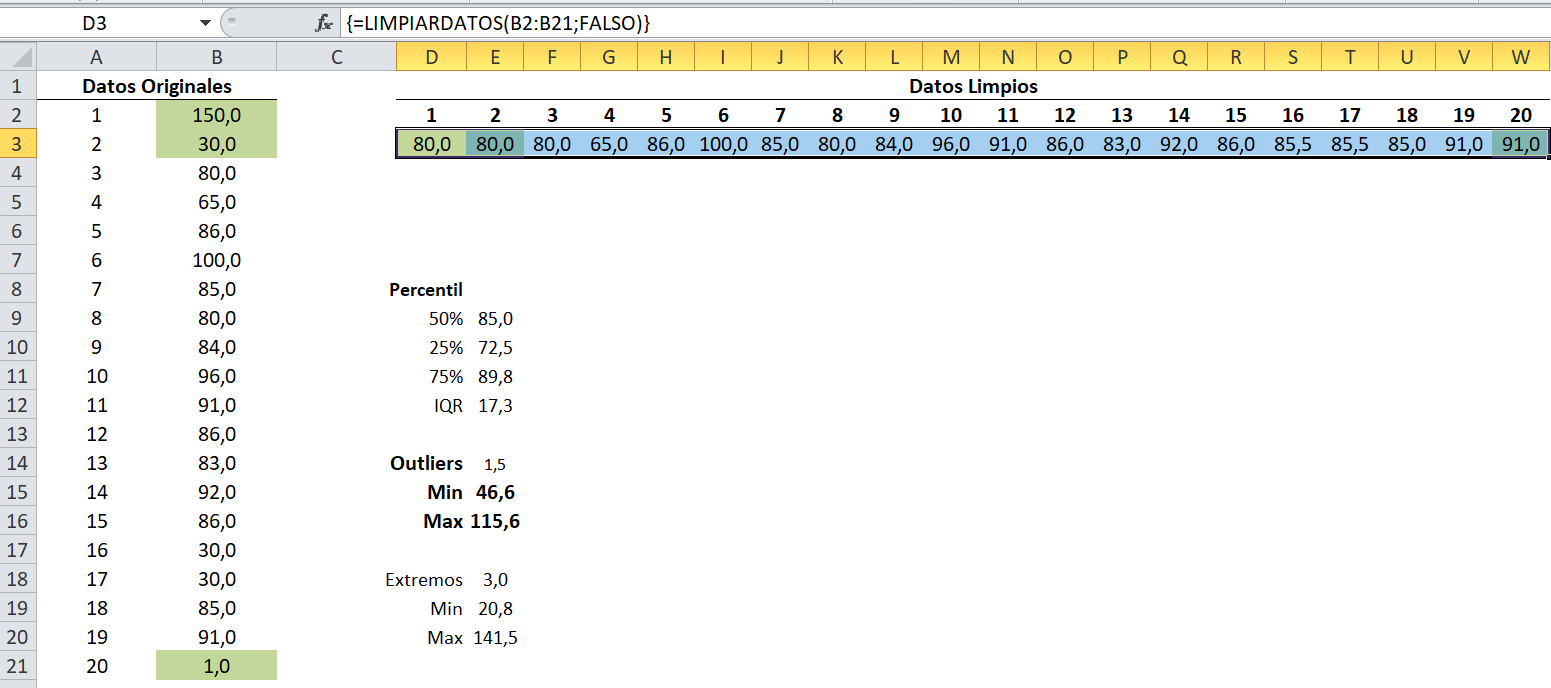
En la imagen se muestra un ejemplo de uso de la función LIMPIARDATOS. A la izquierda, en la columna B se encuentra una serie de datos que se desea proyectar. Considerando 1,5 * IQR, los límites de la población típica son 69,1 y 102,1 respectivamente. De esta manera, sabemos que la serie posee 3 valores atípicos (outliers) marcados en verde, los cuales serán considerados para su eliminación dado que escogimos la opción 0 (FALSO) como segundo parámetro.

A la derecha, se despliega en la fila 3 el resultado del proceso de limpieza. Se visualiza cómo cada uno de los outliers fue reemplazado por el promedio de los valores representativos más cercanos.

Un segundo ejemplo se muestra a continuación con outliers ubicados justo en los extremos del arreglo. Se observa cómo en este caso sólo se considera el valor típico más cercano para reemplazarlo:

Y bueno, hasta aquí la entrega de hoy, espero que hayas disfrutado de su lectura y que puedas usar esta función para limpiar tus datos en lo sucesivo. ¿Qué potenciales mejoras o modificaciones se te vienen en mente?

VBA Evaluar Derivada

Posted on by YorsH

Para ciertas aplicaciones en Excel, como la búsqueda de un valor objetivo a través de una función determinada, nos sería de gran utilidad poder conocer la derivada de un función cualquiera en un punto dado. Imaginemos por ejemplo, el siguiente problema:

Hemos llamado «x» al rango C2 donde podemos cambiar el valor de x sobre el cual queremos evaluar la función y su derivada. Mientras que en F(x), la celda C3, describimos la función a evaluar en términos de la variable anteriormente definida:

Si la fórmula F(x) es una función cualquiera, que puede ser cambiada por el usuario o mediante código, ¿cómo calcular la derivada dF/dx para cualquier x?

Comenzaremos suponiendo que F(x) es una función continua y diferenciable en x, lo que nos permitirá estimar una derivada en x mediante la suma y resta de un diferencial que llamaremos delta:

De forma tal que dF/dx evaluada en x0 estará dada por:

Lo primero que haremos será definir una función en VBA que nos permita evaluar una función cualquiera dada por el usuario para un valor de x arbitrario.

Utilizaremos para ello la función EVALUATE disponible en VBA, que nos permite calcular el valor de una fórmula existente en un rango. El truco consiste en combinar este método con un REPLACE que troque el valor de x por el valor deseado cada vez que lo encuentre en la función. El código en VBA queda como sigue:

Public Function EVALUARFUNCION(Funcion As Range, X As Double) As Double

    'Evalua la formula especificada reemplazando
    'donde diga 'X' por el valor especificado

    Dim Evaluacion As String
    
    Evaluacion = Replace(Funcion.Formula, "x", Str(X))
    EVALUARFUNCION = Evaluate(Evaluacion)
    
End Function

Podemos probar esta nueva función directamente en Excel, verificando que entregue el valor esperado:

Finalmente, podemos usar el código anterior para evaluar F(X) tanto en (x+delta) como en (x-delta) y computar de esta forma la derivada que buscamos. El código en VBA quedará, entonces, como sigue:

Public Function DERIVADA(Funcion As Range, X As Double, Delta As Single) _  
   As Double

   'Aproxima la derivada de la función evaluada en X
   'mediante un Delta suficientemente pequeño

   Dim FXmas As Double
   Dim FXmenos As Double

   FXmas = EVALUARFUNCION(Funcion, X + Delta)
   FXmenos = EVALUARFUNCION(Funcion, X - Delta)

   DERIVADA = (FXmas - FXmenos) / (2 * Delta)

End Function

Podemos probar nuestra nueva función directamente en Excel y ensayarla tanto con nuevos valores de x como con distintas funciones diferenciables en x.

¿Qué nuevas mejoras o aplicaciones se te vienen a la mente? ¡Nos vemos!

VBA Distribución Triangular

Posted on by YorsH

Distribución Triangular

La generación de valores aleatorios en Excel está limitada a las distribuciones que se encuentran disponibles para ser modeladas (Normal, Beta, Binomial, entre otras). Por ejemplo, la siguiente fórmula permite generar números aleatorios distribuidos normalmente en torno a una media y con una desviación estándar especificadas:

=NORM.INV(ALEATORIO(),media,desviacion)

En muchos modelos con pronósticos representados por variables aleatorias, sin embargo, se requiere una distribución sencilla y acotada que permita establecer valores mínimos, máximos y esperados. La Distribución Triangular es la que mejor se acomoda a este requerimiento, pero no se encuentra disponible entre las funciones de Excel.

El siguiente programa en VBA soluciona este problema, creando una nueva función TRIANGULAR(probabilidad, mínimo, máximo, esperado) que genera números aleatorios distribuidos de la forma deseada. El núcleo del algoritmo se basa en las ecuaciones:

Se comienza calculando un número k que representa la posición relativa del punto b (valor esperado) en el intervalo [a,c], por lo cual b pertenecerá al intervalo [0,1]. Luego se genera un valor aleatorio p que también estará entre [o,1[ y se verifica si está antes o después del valor esperado. Si p es menor que k, el valor aleatorio se sitúa a la derecha de a y como función de p. Si p es mayor que k, el valor aleatorio se sitúa a la izquierda de c y como función de (1-p).

De esta forma, la implementación en VBA es muy sencilla y se reduce al siguiente código que define la función TRIANGULAR (no olvidar insertar el código en un Módulo para que pueda ser invocada desde Excel).

Public Function TRIANGULAR(a As Double, b As Double, c As Double, _
   P As Single) As Double

   Dim k As Single
   Dim X As Double

   'Calculamos k
   k = (b - a) / (c - a)

   If P < k Then
      X = a + Sqr(P * (b - a) * (c - a))
   Else
      X = c - Sqr((1 - P) * (b - a) * (c - a))
   End If

   TRIANGULAR = X

End Function

En la planilla de ejemplo vemos un posible uso de la función recién creada, para proyectar valores inciertos de cantidad, costo y margen unitario. Se dispone en las celdas F5 y G5 de los valores máximos y mínimos respectivamente, mientras que en E5 se encuentra el valor esperado. El cuarto parámetro es el valor aleatorio entre [0,1[ que lo generamos mediante la función ALEATORIO() de Excel. La ventaja de hacerlo de esta manera es que generaremos nuevos valores aleatorios cada vez que presionemos F9.

En cambio, si quisiéramos que el valor aleatorio quedara estático (no se modificara en nuestra planilla al presionar al hacer nuevos cálculos), la solución está en eliminar este cuarto parámetro y calcular dentro del procedimiento el valor de P, insertando simplemente la instrucción.

P = RND()

¡Cuéntame qué nuevos usos o mejoras se te vienen en mente!