Derivada | Algoritmos

VBA Newton Raphson

Posted on junio 21, 2019 by YorsH

La gran mayoría de nuestros modelos financieros son construidos para contestar diversas preguntas en torno a puntos de equilibrio: ¿cuál es el nivel de ventas mínimo para que el negocio sea rentable? ¿cuál es la tarifa mínima que consigue pagar los gastos y la inversión?

Lo que hacemos es identificar la función cuyo valor queremos llevar a cierto objetivo (la rentabilidad, por ejemplo) y aislamos una variable cuyo impacto en la función sea relevante (la tarifa, por nombrar alguna).

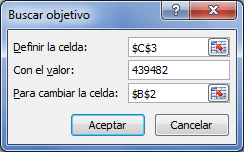
La herramienta buscar objetivo de Excel es de gran utilidad en este punto, aunque debamos volver a utilizarla cada vez que realizamos un cambio en alguna de las otras variables del modelo para obtener un nuevo punto de equilibrio.

¿Cómo evitar este paso y generar modelos que lleguen dinámicamente al equilibrio definido?

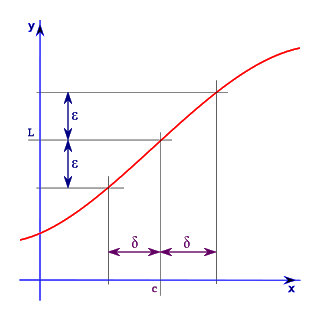
Comencemos recordando el algoritmo de Newton-Raphson para encontrar una raíz de una función determinada:

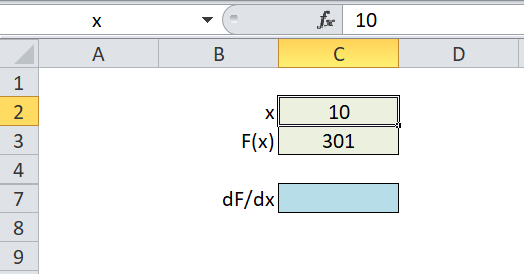
Dos son los problemas que requieren más atención desde el punto de vista del código: calcular la derivada de la función en el nuevo punto de iteración y evaluar la función en ese punto.

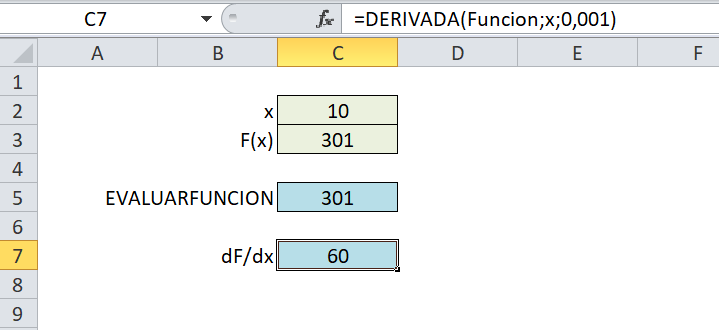
El primero de los problemas, calcular la derivada de una función, lo hemos solucionado en el post anterior, aproximando su valor a la división [f(x+e)-f(x-e)]/2e, para algún valor de e muy pequeño.

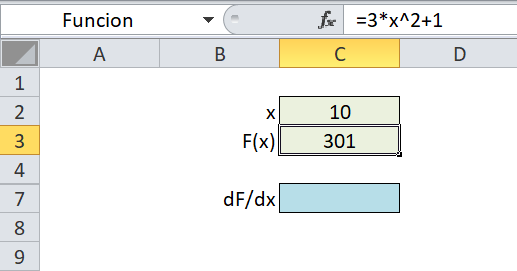
Como en el post anterior la función objetivo era explícita respecto de la variable independiente ‘x’, podíamos evaluarla simplemente reemplazando el carácter ‘x’ en la fórmula por el valor correspondiente, cuantas veces apareciera. Sin embargo, no es necesariamente el caso de este ejemplo, en que la variable independiente puede influir indirectamente sobre la función objetivo.

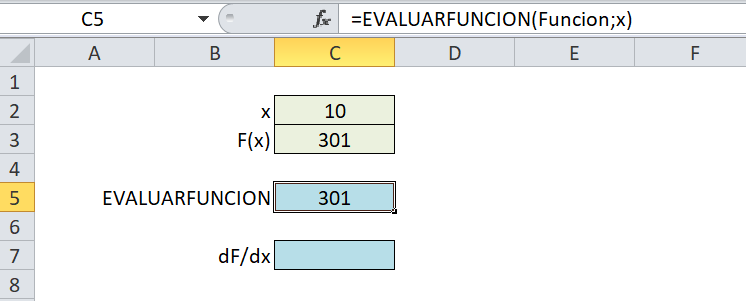
Por este motivo, evaluaremos la función directamente a partir del modelo Excel disponible, leyendo el resultado de la fórmula en la planilla y cambiando para ello en la misma planilla el valor de la variable independiente a ensayar.

Dadas estas restricciones adicionales ya no podemos programar una función iterativa sino un procedimiento que lea y escriba en rangos específicos de la planilla que contiene nuestro modelo. Una versión de este algoritmo en VBA podría ser el siguiente:

Public Sub METODONEWTON()

   On Error Resume Next

   Dim rngFuncion As Range
   Dim rngX As Range
   Dim dblK As Double
   Dim sngDelta As Single
   Dim intIteraciones As Integer

   Dim dblXi As Double
   Dim dblFXi As Double
   Dim dblFXiMAS As Double ' f(Xi + e)
   Dim dblFXiMENOS As Double ' f(Xi - e)
   Dim dblDFDX As Double 'dF/dx evaluado en xi
   Dim intI As Integer

   Const EPSILON = 0.001

   'Itera sobre valores de X mediante el algoritmo de Newton-Raphson 
   'para   encontrar un X* tal que
   '|f(X*)-k| <= delta hasta un máximo de iteraciones especificadas

   'Declaramos variables intermedias
   Set rngFuncion = Range("Funcion")
   Set rngX = Range("X")
   dblK = Range("Objetivo").Value
   sngDelta = Range("Delta").Value
   intIteraciones = Range("Iteraciones").Value

   'Inicializamos las variables
   dblXi = rngX.Value 'valor entregado por el user
   dblFXi = EVALUARFUNCION(rngFuncion, rngX, dblXi)
   intI = 0

   Do Until Abs(dblFXi - dblK) <= sngDelta Or intI >= intIteraciones

      'Calculamos la derivada de f(Xi) en Xi
      dblFXiMENOS = EVALUARFUNCION(rngFuncion, rngX, dblXi - EPSILON)
      dblFXiMAS = EVALUARFUNCION(rngFuncion, rngX, dblXi + EPSILON)
      dblDFDX = (dblFXiMAS - dblFXiMENOS) / (2 * EPSILON)

     'Calculamos el nuevo Xi
      dblXi = dblXi + (dblK - dblFXi) / dblDFDX
      dblFXi = EVALUARFUNCION(rngFuncion, rngX, dblXi)

      intI = intI + 1

   Loop

   'Llegando a este punto ocurrió una de dos: o encontramos el valor    
   'o se acabaron las iteraciones

   If Abs(dblFXi - dblK) <= sngDelta Then
      Range("X").Value = dblXi
   Else
      MsgBox "No se encontró solución"  
      Range("X").Value = dblXi
   End If

End Sub

El núcleo del algoritmo anterior es el método de cálculo de derivadas mencionado dblDFDX = (dblFXiMAS – dblFXiMENOS) / (2 * EPSILON) , mientras que el nuevo método EVALUARFUNCION cuenta con tres parámetros: rngFuncion (la celda en Excel que almacena o redirecciona a la función a evaluar del modelo), rngX (la celda en Excel que contiene la variable independiente del modelo) y dblX (el valor en que queremos evaluar la función).

Un nuevo código para EVALUARFUNCION puede ser el siguiente:

Public Function EVALUARFUNCION(rngFormula As Range, rngX As Range, _
   dblX As Double) As Double

   'Evalúa la formula especificada cambiando donde diga X por dblX

   'Copiamos el valor preexistente en la variable independiente
   Dim dblAnterior As Double
   dblAnterior = rngX.Value

   'Reemplazamos el valor de la variable independiente por dblX
   rngX.Value = dblX

   'Leemos el nuevo valor que toma la función a evaluar
   Application.Calculate
   EVALUARFUNCION = rngFormula.Value

   'Devolvemos el valor preexistente en la variable independiente
   rngX.Value = dblAnterior

End Function

De esta forma, el código puede ser utilizado para encontrar el punto de equilibrio usando nuestra variable independiente cada vez que lo ejecutemos. Para ello, bien podemos usar un botón que lo ejecute cada vez que resulte necesario o podemos vincularlo a alguna otra acción realizada por el usuario para que se ejecute en forma «autónoma».

No es posible vincular la ejecución del procedimiento al método ‘Calculate’ de la hoja, pues genera una redundancia que nos llevaría a desbordar la memoria. El evento que me parece más idóneo es Worksheet_SelectionChange , que invocará al código cada vez que el usuario seleccione un lugar distinto de la hoja. Para ello incrustamos en la hoja que tenemos alojada el modelo las siguientes tres líneas:

Private Sub Worksheet_SelectionChange(ByVal Target As Range)

   If Range("Automatico").Value = "Sí" Then METODONEWTON

End Sub

Comparto, por ejemplo, una implementación simple en la evaluación de un flujo de caja. La sección en gris contiene las variables del modelo: X (C2) es la variable independiente y hacia ella apunta en este caso la celda B12 equivalente a la tarifa a cobrar. La celda B18 contiene el VAN como resultante del modelo, hacia ella apunta C3 que es la celda Función del algoritmo.

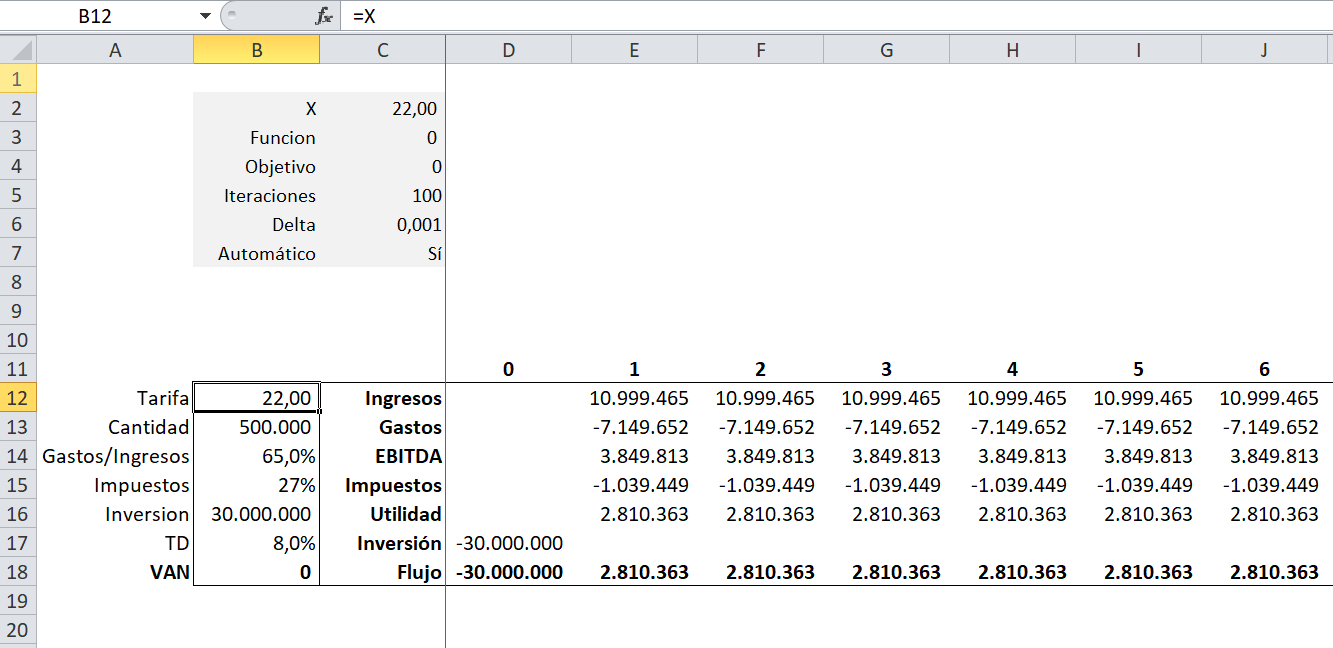
En la celda C7 hemos ubicado un Flag «Sí» / «No» que permite activar o desactivar la ejecución automática (Range ‘Automatico’), devolviéndole el control al usuario para realizar ajustes (como cambiar la variable independiente o la función) o bien para modelar fuera del punto de equilibrio dado por la variable «Objetivo».

¿Qué otras aplicaciones o mejoras se te vienen en mente? No dudes en dejar tus comentarios.

VBA Evaluar Derivada

Posted on junio 19, 2019 by YorsH

Para ciertas aplicaciones en Excel, como la búsqueda de un valor objetivo a través de una función determinada, nos sería de gran utilidad poder conocer la derivada de un función cualquiera en un punto dado. Imaginemos por ejemplo, el siguiente problema:

Hemos llamado «x» al rango C2 donde podemos cambiar el valor de x sobre el cual queremos evaluar la función y su derivada. Mientras que en F(x), la celda C3, describimos la función a evaluar en términos de la variable anteriormente definida:

Si la fórmula F(x) es una función cualquiera, que puede ser cambiada por el usuario o mediante código, ¿cómo calcular la derivada dF/dx para cualquier x?

Comenzaremos suponiendo que F(x) es una función continua y diferenciable en x, lo que nos permitirá estimar una derivada en x mediante la suma y resta de un diferencial que llamaremos delta:

De forma tal que dF/dx evaluada en x0 estará dada por:

Lo primero que haremos será definir una función en VBA que nos permita evaluar una función cualquiera dada por el usuario para un valor de x arbitrario.

Utilizaremos para ello la función EVALUATE disponible en VBA, que nos permite calcular el valor de una fórmula existente en un rango. El truco consiste en combinar este método con un REPLACE que troque el valor de x por el valor deseado cada vez que lo encuentre en la función. El código en VBA queda como sigue:

Public Function EVALUARFUNCION(Funcion As Range, X As Double) As Double

    'Evalua la formula especificada reemplazando
    'donde diga 'X' por el valor especificado

    Dim Evaluacion As String
    
    Evaluacion = Replace(Funcion.Formula, "x", Str(X))
    EVALUARFUNCION = Evaluate(Evaluacion)
    
End Function

Podemos probar esta nueva función directamente en Excel, verificando que entregue el valor esperado:

Finalmente, podemos usar el código anterior para evaluar F(X) tanto en (x+delta) como en (x-delta) y computar de esta forma la derivada que buscamos. El código en VBA quedará, entonces, como sigue:

Public Function DERIVADA(Funcion As Range, X As Double, Delta As Single) _  
   As Double

   'Aproxima la derivada de la función evaluada en X
   'mediante un Delta suficientemente pequeño

   Dim FXmas As Double
   Dim FXmenos As Double

   FXmas = EVALUARFUNCION(Funcion, X + Delta)
   FXmenos = EVALUARFUNCION(Funcion, X - Delta)

   DERIVADA = (FXmas - FXmenos) / (2 * Delta)

End Function

Podemos probar nuestra nueva función directamente en Excel y ensayarla tanto con nuevos valores de x como con distintas funciones diferenciables en x.

¿Qué nuevas mejoras o aplicaciones se te vienen a la mente? ¡Nos vemos!